Las dos circunferencias son tangentes en A , el centro de la mayor es B, CD=42, EF=24. Averigua sus radios.

<https://twitter.com/ilarrosac/status/991728056606887936>

¿Qué fracción del área del hexágono representa la zona sombreada, si los cuatro trozos en que se ha dividido el lado inferior derecho son iguales? 

<https://twitter.com/solvemymaths/status/990911682129154048>

¿Cuántos vigilantes son suficientes para vigilar una galería de arte poligonal? En 1975, Chvátal encontró que cualquier galería poligonal de N vértices se puede vigilar utilizando como máximo N/3 vigilantes. Por ejemplo, cualquier galería de 13 vértices necesitará como máximo 4 (13/3=4'333...) vigilantes. Eso asegura el Teorema de la Galería de Arte, de Chvátal. Eso, y que siempre es posible encontrar un polígono de N vértices que necesite exactamente N/3 vigilantes.

La demostración de este teorema que más ha trascendido, por su elegancia y sencillez, es la que ha hecho Fisk, en 1978:

Lo primero que observa Fisk es que un triángulo sólo necesita un vigilante en uno de sus vértices. Así, lo que propone hacer es dividir la galería en triángulos, asegurar la vigilancia en cada unos de esos triángulos y con ello tendrá asegurada la vigilancia del polígono completo.

En primer lugar, lo que hay que hacer es triangular el polígono ¿Cómo? Añadiendo diagonales interiores uniendo vértices no consecutivos del polígono, siempre que no corten a otra diagonal ya dibujada o a la frontera del polígono.

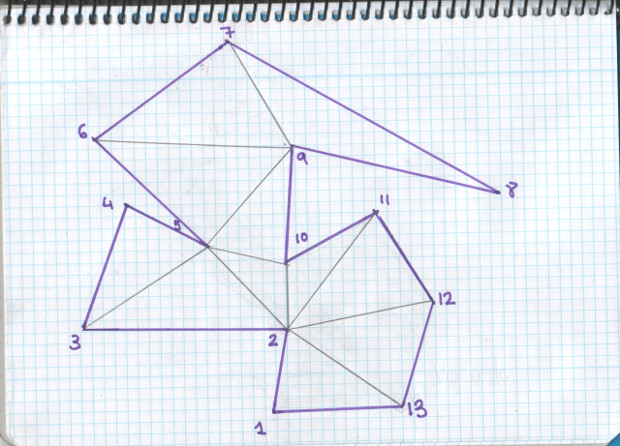
A continuación asignamos colores a los vértices del polígono con la condición de no pintar del mismo color dos vértices adyacentes. Pues bien, respetando esta regla, Fisk demuestra que se puede colorear la triangulación del polígono con 3 y sólo 3 colores.

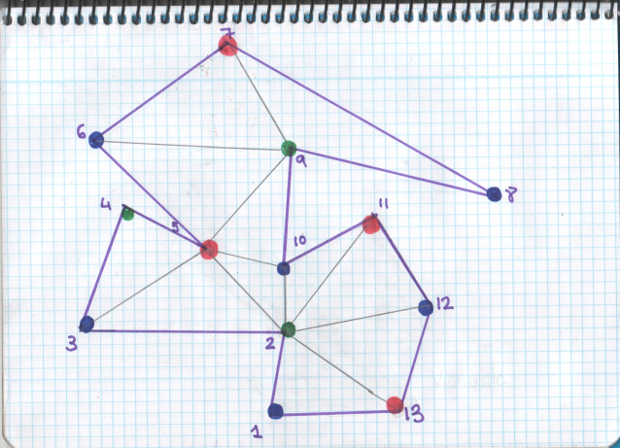
Ahora contamos cuántos vértices hay de cada uno de los tres colores. En el ejemplo que estamos considerando, tenemos 6 vértices azules, 4 vértices rojos, y 3 vértices verdes. Elegimos el color menos común de los tres, en este caso el verde, y colocamos un vigilante en cada uno de los 3 vértices verdes y ya está todo el polígono vigilado ¿Por qué? Pues, porque todos los triángulos del polígono tienen que tener un vértice verde (en realidad, todos los triángulos tienen un vértice de cada uno de los colores) y como en todos los vértices verdes hay un vigilante, todos los triángulos estarán vigilados.

Para finalizar, ¿cómo sabemos que el color menos común de la triangulación aparece como máximo N/3 veces? En el ejemplo anterior, si el color menos común (el verde) apareciese más de 13/3 (4) veces, los tres colores aparecerían más de trece veces, y eso sería imposible.

Lo que sabemos entonces, a partir de este teorema, es que sea cual sea el polígono de N vértices que nos propongan vamos a necesitar, como máximo, N/3 vigilantes para vigilarlo.

<Artículo original: https://blogs.20minutos.es/mati-una-profesora-muy-particular/tag/teorema-de-la-galeria-de-arte>