En un triángulo rectángulo, si a y b son los catetos y c es la altura sobre la hipotenusa, entonces a–2 + b–2 = c–2
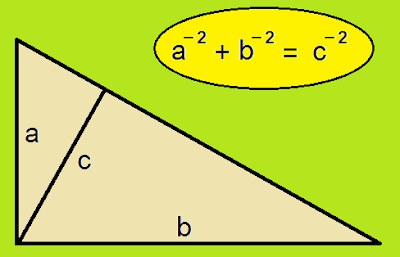
Comprobémoslo:
Si d es la hipotenusa y m y n son las proyecciones de a y b sobre d , por el teorema del cateto (en el primer paso) y por el teorema de la altura (en el último)...
1/a2 + 1/b2 = 1/(md) + 1/(nd) = (m+n) / (mnd) = d / (mnd) = 1 / (mn) = 1/c2
Además, a·b = c·d. Veamos:
El área de un triángulo es igual a (base · altura) / 2. Si apoyamos un triángulo rectángulo sobre un cateto, este es la base y el otro cateto es la altura y tendríamos que el área sería a·b/2 .Si apoyamos el triángulo sobre su hipotenusa d , esta sería ahora la base y c sería la altura, por lo que el área sería también c·d/2 . Y como el área no depende del lado sobre el que se apoye el triángulo... se tiene el resultado.
<Artículo original: http://joselorlop.blogspot.com.es/2018/03/1525.html>


